.jpg)
This is a list of languages, in chronological order, that have been designed under the auspices of Cat's Eye Technologies. For more information on these languages, see below.
The distinction between a Language, a Format, and an Automaton is not always cut-and-dried, so if you can't find what you're looking for here, try those lists as well.
Full Moon Fever
- type: Animation Language
- inception-date: ca 1993
- genre: DSL
- development-stage: archived
- computational-class: known not Turing-complete
- paradigms: Imperative
Sample program:
GO 1 2 CLREOL CENTRE "Enter... the Stupid Guard." 2
GO 1 3 CLREOL
PAUSE 70
GO 76 19
PRINT "0"
PAUSE 20
DO 20
LF PRINT " " LF LF PRINT "0" PAUSE 5;
Full Moon Fever is a language for describing ASCII animations. It was used to deliver animated screens on Chris Pressey's BBS (when it was operational in the early 90's) via ANSI Terminal control codes. This probably counts as his first proper language, even though it wasn't a full programming language, because it had the usual machinery (syntax, parser, interpreter...) Lives on, in a somewhat distended form, as a sub-language of ILLGOL.
The name "Full Moon Fever" has nothing at all to do with lycanthropy; I believe it came from mis-remembering the title of the song "Full Moon Boogie" by Jan Hammer and Jerry Goodman.
Maentwrog
- type: Programming Language
- inception-date: ca 1993
- genre: Pedagogical language
- development-stage: archival
- computational-class: known not Turing-complete
- paradigms: Stack-based
- reference-distribution: Maentwrog distribution
- entry @ esolangs.org
Sample program:
*a *b *c
0 =a 1 =b
: fib a b + =c c . b =a c =b c 100000 < @fib ;
1 . fib
Maentwrog is an RPN-calculator-turned-FORTH-interpreter which probably counts as Chris Pressey's first proper programming language. It was implemented on his Amiga 500 in 1993, then lost and unearthed multiple times. It is hardly remarkable, save that it spawned Befunge-93.
There are no extant example programs from the time the language was first
implemented — I tried writing the Sieve of Eratosthenes in it once,
but never got it to work, probably because == was not
implemented correctly. Recently, example programs and a description of the
language (which has become the provisional spec) have been provided by
Marinus — thanks Marinus!
Also included in the Maentwrog distribution, just for fun, are some other contemporaneous C programs of mine: an RPN calculator which was the predecessor of Maentwrog, a simple recursive-descent expression parser, and a simple cellular automata parser (a distant ancestor of ALPACA, perhaps?)
Maentwrog is the name of a town in Wales, but the usage of its name for this language came via Douglas Adams' "The Meaning of Liff", wherein it is defined thusly: "MAENTWROG (n. Welsh) Celtic word for a computer spelling mistake."
Reference Implementation: maentw.c
- license: Public Domain
- implementation-type: interpreter
- host-language: ANSI C
Befunge-93
- type: Programming Language
- inception-date: Sep 1993
- genre: Esolang
- development-stage: mature
- computational-class: can simulate some push-down automata
- influences: Maentwrog, brainfuck, FALSE
- paradigms: Stack-based, 2-dimensional, Self-modifying
- reference-distribution: Befunge-93 distribution
- entry @ esolangs.org
- online @ archive.org
- jnlp @ archive.org
Sample program:
v <
>?"/",^
>"\",^
Befunge-93 is an esoteric programming language where the program exists in a two-dimensional grid of cells, where each cell contains a single instruction, and execution can proceed in any cardinal direction across this grid — not just left-to-right, but also right-to-left, top-to-bottom, and bottom-to-top.
One of the more popular languages I ever designed and implemented. Eventually begat Befunge-97, Funge-98, and Wierd, and doubtless influenced many others. Cited in the New Hacker's Dictionary.
Reference Implementation: bef
- license: BSD license
- implementation-type: interpreter
- host-language: ANSI C
Implementation: tc.catseye.yoob.befunge93
Wierd
- type: Programming Language
- authors: Chris Pressey, John Colagioia, and Ben Olmstead
- inception-date: 1997
- genre: Esolang
- development-stage: not fully complete
- computational-class: believed Turing-complete
- influences: brainfuck, Befunge-93
- paradigms: Stack-based, 2-dimensional, Angular
- reference-distribution: Wierd distribution
- entry @ esolangs.org
- online @ catseye.tc
Sample program (written by Milo van Handel):
*
*
*
*
* * **
* ** *
** **
* *
* *
* *
* *
* **
* *
* ** *
** *
Wierd is a programming language, inspired somewhat by Befunge-93 and brainfuck, where instructions are not determined by the symbols in a sequence of symbols, but by the bends in a sequence of symbols.
The original Wierd, designed during a three-way email conversation between Chris Pressey, John Colagioia, and Ben Olmstead, is probably lost and gone forever, but two dialects have been specified (sorta) and implemented: Wierd (John Colagioia) and Wierd (Milo van Handel).
Implementation: wierd.c (John Colagioia)
- authors: John Colagioia
- license: Unknown license
- implementation-type: interpreter
- host-language: ANSI C
Implementation: wierd.c (Milo van Handel)
- authors: Milo van Handel
- license: Unknown license
- implementation-type: interpreter
- host-language: ANSI C
Implementation: wierd-jnc.js
- authors: Chris Pressey
- license: Public Domain
- implementation-type: interpreter
- host-language: JavaScript
- host-platform: HTML5
Befunge-97
- type: Programming Language
- inception-date: Dec 25, 1997
- genre: Esolang
- development-stage: lost
- computational-class: ???
- influences: Befunge-93
- paradigms: Stack-based, 2-dimensional, Self-modifying
Product of the Befunge Mailing List Working Group.
Befunge-97 was an unimplemented attempt to design a successor to Befunge-93. The design, however, was not successful — it has been described as "brain-damaged" — primarily due to the fact that separate processes were specified as sharing a single stack.
ALPACA
- type: Programming Language
- inception-date: 1998
- genre: Esolang
- development-stage: mature
- computational-class: ???
- paradigms: Metalanguage, Object-oriented
- reference-distribution: ALPACA distribution
Sample program:
/* John Conway's Game of Life, expressed in ALPACA. */
state Dead " " to Alive when 3 Alive and 5 Dead;
state Alive "*" to Dead when 4 Alive or 7 Dead.
ALPACA is a meta-language for describing cellular automata.
It stands for "A Language for the Pithy Articulation of Cellular Automata". The acronym used to be "A Language for Programming Arbitrary Cellular Automata". This was not quite accurate, as the automata are not in fact arbitrary, so I changed it.
ALPACA is one of the few of my languages in which I've actually implemented other languages (or, well, cellular automata — close enough).
Reference Implementation: alpaca.pl
Reference Implementation: alpaca (Python)
- license: BSD license
- implementation-type: compiler
- host-language: Python
- target-language: JavaScript
Funge-98
- type: Programming Language Family
- inception-date: Sep 11, 1998
- genre: Esolang
- development-stage: mature
- computational-class: Turing-complete
- influences: Befunge-93, Befunge-97
- paradigms: Stack-based, Self-modifying
- reference-distribution: Funge-98 distribution
Sample program:
>>#v?v
^,A' <
^ C'
T
^ <<
G
'
Product of the Befunge Mailing List Working Group.
Funge-98 is a family of programming languages designed as the successor to Befunge-93. It generalizes Befunge-93's two-dimensional nature somewhat, defining languages in one dimension (Unefunge-98), two dimensions (Befunge-98), and three dimensions (Trefunge-98), and suggests possibilities for other dimensions and topologies (but does not specify exactly how they look or would behave.) It also makes the playfield unbounded, allowing the language to be Turing-complete, and tries to define mechanisms for interacting with the operating system and engaging extensions to the language.
Befunge-98
- type: Programming Language
- genre: Esolang
Befunge-98 is the realization of Funge-98 in two dimensions.
Trefunge-98
- type: Programming Language
- genre: Esolang
Trefunge-98 is the realization of Funge-98 in three dimensions.
Unefunge-98
- type: Programming Language
- genre: Esolang
Unefunge-98 is the realization of Funge-98 in one dimension.
MDPN
- type: Meta-language
- inception-date: 1999
- genre: Esolang
- development-stage: not fully complete
- computational-class: ???
- paradigms: Metalanguage
- reference-distribution: Specs on Spec distribution
Sample program:
Box ::= "+" {"-"}^(w) r(-90) "+" "||" {"|"}^(h) r(-90)
"+" {"-"}^(w) r(-90) "+" "||" {"|"}^(h) r(-90)
MDPN is a meta-language for describing multi-directional and multi-dimensional languages.
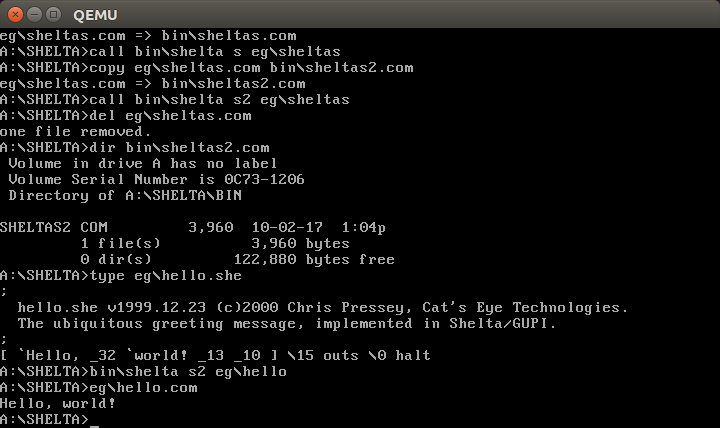
Shelta
- type: Programming Language
- inception-date: ca Jul 1999
- genre: Esolang
- development-stage: mature
- computational-class: ???
- paradigms: Stack-based
- reference-distribution: Shelta distribution
- online @ catseye.tc
Sample program:
[ `Hello, _32 `world! _13 _10 ] \15 outs \0 halt
Shelta is an extremely minimal Forth-like language with barely any semantics; it relies on inline machine code to write anything resembling an actual program in it. In the spirit of compilers for languages such as FALSE and brainfuck, a Shelta-to-8086 compiler was implemented (with help from Ben Olmstead) in less than 512 bytes of 80286 machine code. What's more, it's also been bootstrapped — that is to say, a Shelta compiler was written in Shelta, which was compiled with the original compiler, and then compiled again with the resulting compiler, producing a wholly self-hosted executable!
Reference Implementation: shelta
- license: Freely Redistributable
- implementation-type: compiler
- host-language: NASM Assembler
- target-language: x86 machine code
Implementation: sheltas
- license: Freely Redistributable
- implementation-type: compiler
- host-language: Shelta
- target-language: x86 machine code
Bear Food
- type: Programming Language
- inception-date: ca Dec 1999
- genre: Esolang
- development-stage: lost
- computational-class: ???
- paradigms: Stack-based
Bear Food was a horrible language defined by an interpreter that evolved (no... let's be honest, it devolved) from a small piece of example code showing how to parse and intepret a simple reverse-polish notation language. This same example code also took a very divergent line of evolution, eventually becoming the programming language Var'aq.
Reference Implementation: bearfood.pl
- license: Unknown license
- implementation-type: interpreter
- host-language: Perl
Sally
- type: Programming Language
- inception-date: 2000
- genre: Esolang
- development-stage: mature
- computational-class: ???
- paradigms: Functional
- reference-distribution: Sally distribution
Sample program:
stdlib
int factorial int if $1 mul $1 factorial sub $1 1 1
int main int factorial $1
Sally is a cute but naive little functional language with a minimal syntax, a strict type system, and some unusual rules for parameters and return values.
Reference Implementation: sally2c
ILLGOL
- type: Programming Language
- inception-date: ca Apr 2000
- genre: Joke language
- development-stage: mature
- computational-class: ???
- paradigms: Imperative
- reference-distribution: Illgol: Grand Mal
- entry @ esolangs.org
- online @ catseye.tc
Sample program:
NB eh.ill
10 *f = { print str(#0), EoL };
20 do f(1);
30 don't f;
40 do f(2);
50 reinstate f;
60 do f(3);
FIN
ILLGOL is a joke language which parodies the sort of language designed by the sheer fact that a compiler for it has been hacked together.
Reference Implementation: illgol.exe
- license: Unknown license
- implementation-type: compiler
- host-language: ANSI C
- target-language: x86 machine code
- in-distributions: ILLGOL distribution, Illgol: Grand Mal
Illgola-2
- type: Programming Language
- genre: Joke language
- in-distributions: Illgola-2 distribution, Illgol: Grand Mal
Successor to ILLGOL.
Illberon
- type: Programming Language
- genre: Joke language
- in-distributions: Illberon distribution, Illgol: Grand Mal
Successor to Illgola-2.
Open Sores Illgol##
- type: Programming Language
- genre: Joke language
- in-distributions: Illgol: Grand Mal
Successor to Illberon.
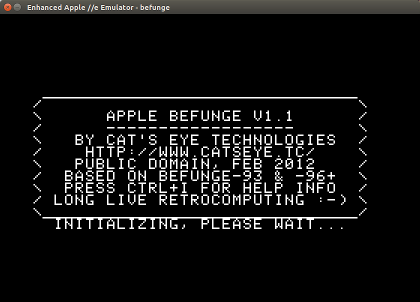
Apple Befunge
- type: Programming Language
- inception-date: Jul 3, 2000
- genre: Esolang
- variant-of: Befunge-93
- development-stage: archival
- paradigms: Stack-based, 2-dimensional, Self-modifying
- reference-distribution: Apple Befunge distribution
- online @ archive.org
Apple Befunge is a variant of Befunge for the Apple ][+ which resembles Befunge-93, with some extra Befunge-96-esque instructions and some Apple ][+-specific instructions.
Reference Implementation: APPLE BEFUNGE EDITOR
- development-stage: archival
- license: Public Domain
- implementation-type: interpreter, editor
- host-language: Applesoft BASIC
- host-platform: Apple II
SMITH
- type: Programming Language
- inception-date: ca Jul 2000
- genre: Esolang
- development-stage: mature
- computational-class: Turing-complete
- influences: SMETANA
- paradigms: Imperative, Self-modifying
- reference-distribution: SMITH distribution
- entry @ esolangs.org
- online @ archive.org
Sample program:
MOV R0, 10
MOV R2, 0
SUB R2, 1
MOV R[R0], "Hello, world!"
MOV TTY, R[R0]
SUB R0, R2
MOV R1, R0
SUB R1, 23
NOT R1
NOT R1
MUL R1, 8
COR +1, -7, R1
SMITH is a self-modifying assembly-like language which completely lacks any kind of jump instructions whatsoever. Despite this handicap, it has been shown to be Turing-complete.
Reference Implementation: smith.pl
- license: BSD license
- implementation-type: interpreter
- host-language: Perl
Tamerlane
- type: Programming Language
- inception-date: Aug 2000
- genre: Esolang
- development-stage: mature
- computational-class: ???
- paradigms: Graph-rewriting, Imperative
- reference-distribution: Specs on Spec distribution
Sample program:
Point-A: 1 Point-B,
Point-B: 1 Point-C,
Point-C: 1 Point-A.
?- 1 Point-A -> 0 Point-A @ Point-A
Tamerlane is a multi-paradigmatic programming language, unimplemented and possibly unimplementable. One of its core execution mechanisms is the traversing of a graph (representing the program) while rewriting that same graph.
Squishy2K
- type: Programming Language
- inception-date: Sep 2000
- genre: Esolang
- development-stage: mature
- computational-class: believed Turing-complete
- paradigms: String-rewriting, State machine
- reference-distribution: Squishy2K distribution
- entry @ esolangs.org
Sample program:
* main { start many finish? "Hello, world!"! }
Squishy2K is a language which is a hybrid of string rewriting and finite state automata; as an added twist, it also lets program states serve as functions. It was based largely on an earlier grammar-based language called SQUISHY, taking also some ideas from the language Thue. The original SQUISHY was conceived sometime around 1998, but is now lost. Because it was based largely on EBNF, the author wanted to name it Wirth, but the name SQUISHY was proposed and (somewhat unfortunately) stuck.
Reference Implementation: squishy2k.pl
- license: Public Domain
- implementation-type: interpreter
- host-language: Perl
HUNTER
- type: Programming Language
- inception-date: ca Sep 20, 2000
- genre: Esolang
- development-stage: mature
- computational-class: ???
- paradigms: 2-dimensional, Maze-space-rewriting
- reference-distribution: HUNTER distribution
- entry @ esolangs.org
- online @ archive.org
Sample program:
##################
# 1#2# #
# #### # #
# # #
# ###### M #
# M# #
#+###### #
# !# #
##################
*12+>3
*21+>3
HUNTER is a language I designed for the Esoteric Awards ("Essies") Its abstract starts out like this:
It is perceived that one of the biggest problems in maintaining interest in programming is the above linear growth of boredom compared to the usefulness of the program, resulting in an acute loss of enthusiasm on the part of the programmers and ultimately the abandonment of the software...
Reference Implementation: hunter.pl
- license: BSD license
- implementation-type: interpreter
- host-language: Perl
'N-DCNC
- type: Programming Language
- inception-date: Oct 2000
- genre: Joke language
- development-stage: not fully complete
- computational-class: ???
- paradigms: Functional
- reference-distribution: 'N-DCNC distribution
- entry @ esolangs.org
Sample program:
4*5+2/2,(9*`c)+1
'N-DCNC was Chris Pressey's entry for the 2000 Esoteric Awards (which might have actually been Esoteric Awards 2001). It is based on a conspiracy theory involving UFOs and a 5-member boy band, or something.
A copy of PortableFalse is included in the 'N-DCNC distribution, to make it easier for you to run the code generated by the 'N-DCNC compilers. However, you still need a C compiler to build the PortableFalse interpreter.
Reference Implementation: ndcnc.pl
- license: Unknown license
- implementation-type: compiler
- host-language: Perl
- target-language: FALSE
Implementation: ndcnc.bf
- license: Unknown license
- implementation-type: compiler
- host-language: Befunge-93
- target-language: FALSE
Broken.
Strelnokoff
- type: Programming Language
- inception-date: Apr 2001
- genre: Esolang
- development-stage: not fully complete
- computational-class: believed Turing-complete
- paradigms: Imperative, Non-deterministic
- reference-distribution: Strelnokoff distribution
- entry @ esolangs.org
- online @ archive.org
Sample program:
REM HELLO WORLD IN STRELNOKOFF
REM CHRIS PRESSEY MARCH 24 2001
X = (X / X) * X + (X = 0) * (T = 0) * (PRINT CHAR 'H' - 'H' + 1)
X = (X / X) * X + (X = 0) * (T = 1) * (PRINT CHAR 'e' - 'e' + 2)
X = (X / X) * X + (X = 0) * (T = 2) * (PRINT CHAR 'l' - 'l' + 3)
X = (X / X) * X + (X = 0) * (T = 3) * (PRINT CHAR 'l' - 'l' + 4)
X = (X / X) * X + (X = 0) * (T = 4) * (PRINT CHAR 'o' - 'o' + 5)
X = (X / X) * X + (X = 0) * (T = 5) * (PRINT CHAR ',' - ',' + 6)
X = (X / X) * X + (X = 0) * (T = 6) * (PRINT CHAR ' ' - ' ' + 7)
X = (X / X) * X + (X = 0) * (T = 7) * (PRINT CHAR 'w' - 'w' + 8)
X = (X / X) * X + (X = 0) * (T = 8) * (PRINT CHAR 'o' - 'o' + 9)
X = (X / X) * X + (X = 0) * (T = 9) * (PRINT CHAR 'r' - 'r' + 10)
X = (X / X) * X + (X = 0) * (T = 10) * (PRINT CHAR 'l' - 'l' + 11)
X = (X / X) * X + (X = 0) * (T = 11) * (PRINT CHAR 'd' - 'd' + 12)
X = (X / X) * X + (X = 0) * (T = 12) * (PRINT CHAR '!' - '!' + 13)
X = (T = X) * 0 + (X > T) * X REM RESET FLAG
T = (X / X) * X + (X = 0) * T REM INCREMENT TICK
Strelnokoff is a non-deterministic imperative programming language. Despite this apparent handicap, it appears to be Turing-complete — thanks to a short-circuiting multiplication operator — but a critical feature, namely arrays, has yet to be implemented.
The name "Strelnokoff" was taken from a fictional brand of vodka featured in a parody advertisement on the television show SCTV.
Reference Implementation: strelnokoff.pl
- license: BSD license
- implementation-type: interpreter
- host-language: Perl
Opus-2
- type: Conlang
- inception-date: Jul 2001
- genre: Abstract Artlang
- development-stage: not fully complete
- computational-class: ???
- reference-distribution: Specs on Spec distribution
Sample utterance:
+ pale green
+ Eb, trombone, forte
+ leaning 40 degrees left (sudden)
+ C, tubular bells, piano
+ mothballs (gentle whiff)
Opus-2 is not a programming language, but rather, an abstract artlang (i.e., a conlang designed independently from any conception of society.) The sole design principle was to entirely eliminate word order.
Ypsilax
- type: Programming Language
- inception-date: Aug 2001
- genre: Esolang
- development-stage: mature
- computational-class: believed Turing-complete
- paradigms: Grid-rewriting, Reflective
- reference-distribution: Ypsilax distribution
- entry @ esolangs.org
- online @ archive.org
- jnlp @ archive.org
Sample program:
( ) ( )
# #
# ### ### #
# #
### ###
# #
# #
# ###
Ypsilax is a non-deterministic, reflective, two-dimensional grid-rewriting language. Rewriting rules look for patterns in the grid and replace them with other patterns. These rules are themselves represented by patterns in the grid, and therefore rules can match and rewrite other rules.
Reference Implementation: ypsilax.pl
- license: BSD license
- implementation-type: interpreter
- host-language: Perl
Implementation: tc.catseye.yoob.ypsilax
Version
- type: Programming Language
- inception-date: Sep 2001
- genre: Esolang
- development-stage: mature
- computational-class: unknown computational class
- paradigms: Imperative, Regular-expression-based
- reference-distribution: Version distribution
- entry @ esolangs.org
- online @ archive.org
Sample program:
START: ROOM = "VALLEY|BROOK|GLADE"
CONT: IGNORE = ROOM
VALLEY: OUTPUT = "You are standing in a valley."
HILL: OUTPUT = "You are on top of a hill."
BROOK: OUTPUT = "You are by a brook."
GLADE: OUTPUT = "You are standing in a sun-dappled glade."
ROOM: OUTPUT = EOL
ROOM: DIR = CHOP INPUT
ROOM: IGNORE = DIR
ROOM: MASK = "VAPOURS"
N: CAT = "|N"
S: CAT = "|S"
E: CAT = "|E"
W: CAT = "|W"
ROOM: IGNORE = MASK
N: ROOM = "VALLEY|BROOK|GLADE"
S: ROOM = "HILL|BROOK|GLADE"
E: ROOM = "VALLEY|HILL|BROOK"
W: ROOM = "VALLEY|HILL|GLADE"
LASTLY: IGNORE = "START"
Version is an imperative programming language that uses ignorance-spaces for flow control; all instructions which match the current ignorance pattern are ignored during execution.
Reference Implementation: version.pl
- license: BSD license
- implementation-type: interpreter
- host-language: Perl
beta-Juliet
- type: Programming Language
- inception-date: ca 2002
- genre: Esolang
- development-stage: mature
- computational-class: believed Turing-complete
- paradigms: Event-oriented
- reference-distribution: beta-Juliet distribution
- entry @ esolangs.org
Sample program:
event WindowSwitchBroken;
event MotionDetectorTriggered;
event SystemArmed;
event SystemDisarmed;
event Alarm,
caused after WindowSwitchBroken when SystemArmed > SystemDisarmed,
caused after MotionDetectorTriggered when SystemArmed > SystemDisarmed,
causes Alarm.
alphabet Domino,
One, Two, Three, Four, Five, Six, Seven;
event Begin,
causes Domino One Falls;
event Domino (N = Domino+) Falls,
causes Domino (succ N) Falls.
beta-Juliet is a minimal event-based language. Each event is caused by some other event. Event causation is conditional based on which of two given events occurred more recently.
Portia is a preprocessor for beta-Juliet which allows large, regular, finite sets of events to be described succinctly.
Version 2.0 of beta-Juliet (formerly known as "2iota") allows infinite sets of events to be specified, allowing the language to be Turing-complete.
Reference Implementation: 2iota
- license: BSD license
- implementation-type: interpreter
- host-language: C99
Implementation: b_juliet.pl
- license: BSD license
- implementation-type: interpreter
- host-language: Perl
Sbeezg
- type: Programming Language
- inception-date: 2002
- genre: Esolang
- development-stage: archival
- computational-class: ???
- paradigms: Functional
- reference-distribution: Sbeezg distribution
- entry @ esolangs.org
Sample program:
f={a,b|i=*is;s=*pred;p=*print;g=p(*beer);h=s(a);
ln={x,m|z=x|x};lg={y,n|q=n(y,n)|y};j=i(h,0,ln,lg);
k=j(h,b)|a};l=f(99,f)
Sbeezg is a syntactically very simple language that attempts to take the single-assignment concept to a logical extreme.
I really don't remember exactly what I was trying to accomplish with this; the basic idea is fairly absurd (either your variables are single-assignment or they're not...)
Reference Implementation: sbeezg.erl
- license: Public Domain
- implementation-type: interpreter
- host-language: Erlang
GraNoLa/M
- type: Programming Language
- inception-date: Jul 2002
- genre: Esolang
- development-stage: mature
- computational-class: ???
- influences: Tamerlane
- paradigms: Graph-rewriting, Imperative
- reference-distribution: GraNoLa/M distribution
Sample program:
a=^sajalom(b=^#d(c=^bimodang(^a))d(e=^#cthulhu(f=^uwaming(g=^ubewic()))))
GraNoLa/M is a Graph-Node-based Language (possibly for Machines.) It was one of my submissions for the Esoteric Awards. Not unlike Tamerlane, its execution model involves both traversing and rewriting a graph at the same time.
Reference Implementation: granolam.erl
- license: Public Domain
- implementation-type: interpreter
- host-language: Erlang
Kangaroo Iceberg
- type: Programming Language
- inception-date: Jul 2004
- genre: Esolang
- development-stage: unfinished
- computational-class: ???
- influences: Tamerlane
- paradigms: Graph-rewriting
- reference-distribution: Kangaroo Iceberg distribution
Sample program:
A { ^A:0 / ^A:0 -> ^A:1 }
B { / ^B:0 -> ^B:1, ^B:1 -> ^B:2 }
C { {}:0 / ^K:0 -> ^K:1, ^K:1 -> ^K:2; ^A:1 -> ^A:0 }
Kangaroo Iceberg was a short-lived attempt to pare down Tamerlane to something implementable, and implement it. Although it got a fair ways along (e.g. the parser for graphs seems to be complete, I lost interest in it at the time, and put off finishing it indefinitely.
Now, the challenge will be reconstructing the language from the partial implementation and notes that I left behind...
Reference Implementation: kiceberg
- license: BSD license
- implementation-type: interpreter
- host-language: ANSI C
Beturing
- type: Programming Language
- inception-date: Oct 20, 2005
- genre: Esolang
- development-stage: mature
- computational-class: Turing-complete
- influences: Befunge-93
- paradigms: Imperative, State machine
- reference-distribution: Beturing distribution
- entry @ esolangs.org
Sample program:
# D(40, 4)
# @(40, 4)
$bbab$
# C(0, 0)
# @(0, 0)
. . . . . .
*v*<*<*<*>*v
aa .ab . .aa .
>/*>./*^*^</*v
bb .ba . .bb .
>/*^./*^*^</*v
$$ .$$ . .$$ .
>/*^</*>*^.@*v
. . .
*@ *^*<*<
Beturing is a "Befunge-flavoured" language for describing Turing machines; both the tape and the finite control are laid out two-dimensionally. In addition, the finite control must be expressed as a planar graph (no edge representing a transition may cross any other edge.) It was devised this way as a test of the so-called "wire-crossing problem". It turns out that there are universal Turing machines with finite controls that are planar graphs, so Beturing is Turing-complete.
Reference Implementation: beturing.lua
- license: BSD license
- implementation-type: interpreter
- host-language: Lua
Bhuna
- type: Programming Language
- inception-date: Oct 21, 2005
- genre: Production language
- development-stage: archival
- computational-class: believed Turing-complete
- influences: Lua
- paradigms: Imperative, Functional
- reference-distribution: Bhuna distribution
Sample program:
Fib = ^ X {
if X < 2 return 1 else
return Fib(X - 1) + Fib(X - 2)
}
Print Fib(32), EoL
Bhuna is a small, garbage-collected language with a simple syntax, closures, inferred types, lightweight processes, and support for UTF-8 source code. It was implemented partly to see how closely I could match the performance of Lua's interpreter. It was meant more more as an experimental starting point for branching new languages, than as a useful language in and of itself.
Reference Implementation: bhuna
- license: BSD license
- implementation-type: interpreter
- host-language: C99
Kosheri
- type: Programming Language
- inception-date: ca 2007
- genre: Production Language
- development-stage: unfinished
- etymology: Egyptian street food
- reference-distribution: Kosheri distribution
Kosheri is a virtual machine design that rose from the ashes of Bhuna.
Reference Implementation: kosheri (C)
- license: Unknown license
- implementation-type: interpreter
- host-language: C99
Burro
- type: Programming Language
- inception-date: 2007
- genre: Esolang
- development-stage: not fully complete
- computational-class: Turing-complete
- influences: brainfuck
- paradigms: Imperative, Algebraic
- reference-distribution: Burro distribution
- entry @ esolangs.org
- online @ catseye.tc
Sample program:
!--(--(--(!>/
>>--(+<<+++++++>/+++>+++++>)<
>)/
>>--(+++>+++++>/+++<<<<<+++>)<
>)/
>>--(+++>+>/+<<+++>)<
>)<
Burro is a brainfuck-like programming language whose programs form an algebraical group (modulo the equivalence relation of "computes the same function") under the operation of concatenation. The upshot of this is that, for every Burro program, we can find an antiprogram which, when appended to the program, forms a "no-op" program which has no effect. This is a form of reversible computing, but unlike most reversible languages where it is the execution of the program that is "undone", in Burro, it is the program itself which is annihiliated by its antiprogram. Burro 1.0 was released in fall of 2007, but proved not to form a proper group. This shortcoming was rectified in summer of 2010.
Reference Implementation: Burro.lhs
- license: BSD license
- implementation-type: interpreter
- host-language: Haskell
Hev
- type: Programming Language
- inception-date: May 23, 2007
- genre: Esolang
- development-stage: mature
- computational-class: believed Turing-complete
- paradigms: Term-rewriting
- reference-distribution: Hev distribution
- entry @ esolangs.org
Sample program:
71+8*27,19,29*99,6,37,7,61,47
Hev is a programming language that attempts to solve the "central problem of infix notation": how do you allow it without requiring the programmer to either memorize precedence tables or litter parentheses everywhere? Hev has a way! In Hev, all operators are infix, yet no tiresome memorization of any dreadful precedence table is required!
Reference Implementation: Hev.hs
- license: BSD license
- implementation-type: interpreter
- host-language: Haskell
Cabra
- type: Programming Language
- inception-date: Oct 30, 2007
- genre: Esolang
- development-stage: not fully complete
- computational-class: known not Turing-complete
- influences: Burro
- paradigms: Imperative, Algebraic
- reference-distribution: Cabra distribution
Sample program:
(SET 1 + SET 2) * IFSET 1 THEN (IFSET 2 THEN SET 3 ELSE SKIP) ELSE SKIP
Cabra is a (somewhat) formal programming language whose programs form an algebraical dioid (an idempotent semiring), modulo the equivalence relation of "computes the same function", under the operations of parallel execution (as the additive operator) and sequential composition (as the multiplicative operator).
Reference Implementation: cabra.hs
- license: BSD license
- implementation-type: interpreter
- host-language: Haskell
You are Reading the Name of this Esolang
- type: Programming Language
- inception-date: Nov 2007
- genre: Esolang
- development-stage: mature
- computational-class: Turing-complete
- influences: Spoon
- paradigms: Imperative
- reference-distribution: Specs on Spec distribution
- entry @ esolangs.org
Sample program:
001000000[0010000000111001000011]11100100001[0]
You are Reading the Name of this Esolang is an exploration in the design space of programming languages with undecidable elements. Its syntax is only recursively enumerable: the problem of determining whether or not a given string of symbols is a well-formed You are Reading the Name of this Esolang program is undecidable.
The description makes it sound a bit more mind-blowing than it actually is. In fact C++ has essentially the same property: it's template system is Turing-complete. In practice, this means you can hang the compiler with templates that expand unboundedly (and the compiler has no means by which to detect all possible compiler-hanging-templates.)
Emmental
- type: Programming Language
- inception-date: Nov 11, 2007
- genre: Esolang
- development-stage: mature
- computational-class: believed Turing-complete
- paradigms: Meta-circular, Reflective
- reference-distribution: Emmental distribution
- entry @ esolangs.org
- online @ catseye.tc
Sample program:
;#58#126#63#36!;#46#36#!;#0#1!;#0#2!;#0#3!;#0#4!;#0#5!;#0#6!;#0#7!#0#33#111#108#108#101#72$
Emmental is a self-modifying programming language. It is defined in terms of a meta-circular interpreter, and this meta-circular interpreter provides an operation that redefines operations of the meta-circular interpreter. In fact, this mechanism is required for Emmental to be Turing-complete.
Emmental was followed up by Mascarpone, which tried to make this self-modifying mechanism cleaner.
Reference Implementation: Language.Emmental
- license: Public Domain
- implementation-type: interpreter
- host-language: Haskell
Iphigeneia
- type: Programming Language
- inception-date: Nov 25, 2007
- genre: Pedagogical language
- development-stage: mature
- computational-class: ???
- paradigms: Imperative, Functional
- reference-distribution: Iphigeneia distribution
Sample program:
var a in a :=
let c = 5 in let d = 1 in
loop
if c = 0 then
d
else
let d = d * c in
let c = c - 1 in
repeat
Iphigeneia is a toy programming language which contains features
from both imperative programming (assignments to mutable variables, while
loops,) and functional programming (immutable name bindings, Scheme-style
"named let" loops.) It was originally intended as a testbed for algorithms
that convert programs between the two forms.
Reference Implementation: iphi
- license: BSD license
- implementation-type: interpreter
- host-language: Haskell
Mascarpone
- type: Programming Language
- inception-date: Dec 10, 2007
- genre: Esolang
- development-stage: mature
- computational-class: believed Turing-complete
- influences: Emmental
- paradigms: Meta-circular, Reflective
- reference-distribution: Mascarpone distribution
- entry @ esolangs.org
- online @ catseye.tc
Sample program:
v['[/''/']v*]v*'?<^v[/?/<]v*'S<[>!]v*'F<^[]v*1'p'kS'kF.
Mascarpone is a self-modifying language able to alter the meta-circular interpreter which defines it, like its predecessor Emmental. Unlike Emmental however, in Mascarpone interpreters are first-class objects, making the job of reflective interpreter-modification quite a bit cleaner and richer.
Reference Implementation: Language.Mascarpone
- license: Public Domain
- implementation-type: interpreter
- host-language: Haskell
Larabee
- type: Programming Language
- inception-date: Jan 10, 2008
- genre: Esolang
- development-stage: mature
- computational-class: known not Turing-complete
- paradigms: Imperative
- reference-distribution: Larabee distribution
- entry @ esolangs.org
Sample program:
(store (input) (input)
(store (input) (input)
(label loop
(store (input) (op * (fetch (input)) (fetch (input)))
(store (input) (op - (fetch (input)) (input))
(test (op > (fetch (input)) (input))
(goto loop) (print (fetch (input)))))))))
Larabee is an assembly-like programming language, with Scheme-like syntax, that borrows the notion of branch prediction from computer architecture and abuses it, creating a path that leads only to existential angst and self-destruction.
Reference Implementation: larabee.scm
- license: BSD license
- implementation-type: interpreter
- host-language: Scheme
Arboretuum
- type: Programming Language
- inception-date: Mar 2008
- genre: Experimental language
- development-stage: mature
- computational-class: believed Turing-complete
- paradigms: Forest-rewriting
- reference-distribution: Arboretuum distribution
Sample program:
(
(
(ast: (let a 4 (+ 3 (* a 3))) )
(stab: eot)
(out: halt)
)
(
((ast: (let #(n sym) #(v) #(expr)) => #(expr) )
(stab: eot => (#(n) #(v) EOT) ))
((ast: #(n sym) => #(v) )
(stab: (#(n) #(v) #(tab)) => (#(n) #(v) #(tab)) ))
((ast: #(a num) => _ )
(out: halt => (push #(a) halt) ))
((ast: (+ _ _) => _ )
(out: halt => (add halt) ))
((ast: (* _ _) => _ )
(out: halt => (mul halt) ))
)
)
Arboretuum is an experimental language based on forest-rewriting, a variant of tree-rewriting in which multiple trees are rewritten simultaneously. The language was intended for specifying compilers, with each tree representing a major compiler data structure (AST, symbol table, output buffer, etc.,) however, this idea was not entirely successful. Regardless, Arboretuum is Turing-complete, as tree-rewriting is simply a special case of forest-rewriting.
Reference Implementation: forest-rewriter.scm
- license: Public Domain
- implementation-type: interpreter
- host-language: Scheme
Treacle
- type: Programming Language
- inception-date: Apr 12, 2008
- genre: Experimental language
- development-stage: mature
- computational-class: believed Turing-complete
- influences: Arboretuum
- paradigms: Term-rewriting
- reference-distribution: Treacle distribution
Sample program:
(
(:i (? t (x (? i *) (? j *)))) -> (t : (xx (? j *) (? i *)))))
(:i (? p right)) -> (p : left)
)
Treacle is an experimental compiler-definition language based on context rewriting, an expressive variant of term rewriting that generalizes the forest-rewriting used by its predecessor Arboretuum. In context rewriting, a separation is made between names and variables, and patterns may contain holes inside which subpatterns may match at any depth.
Reference Implementation: treacle.scm
- license: BSD license
- implementation-type: interpreter
- host-language: Scheme
Quylthulg
- type: Programming Language
- inception-date: Dec 6, 2008
- genre: Esolang
- development-stage: mature
- computational-class: believed Turing-complete
- paradigms: Functional
- reference-distribution: Quylthulg distribution
- entry @ esolangs.org
- online @ catseye.tc
Sample program:
foreach $n$=:L:[1,2,3|goto$L$] with $a$=1 be +$a$+$n$+ else be abort
Quylthulg is a programming language with but a single control-flow
construct: foreach. In fact, it does also have a goto, but that can
only appear inside data structures.
Reference Implementation: Qlzqqlzuup, the Lord of Flesh
- license: BSD license
- implementation-type: interpreter
- host-language: Haskell
Zame
- type: Programming Language
- inception-date: Jan 2009
- genre: Esolang
- variant-of: Etcha
- paradigms: Maze-space-rewriting (kind of)
Sample program:
#########
# # #
# # # ###
# # #
### # # #
# # # #
#########
Zame is an automaton which uses the solution of a maze to generate an Etcha program which draws a new maze, then the process repeats. An open question is to find a maze for which this process repeats indefinitely.
Where it stands relative to other models of computation is, therefore, not well understood.
Information on this language is only available on the Esowiki for now: Zame.
This is actually a language family.
Unlikely
- type: Programming Language
- inception-date: Mar 15, 2009
- genre: Esolang
- development-stage: not fully complete
- computational-class: believed Turing-complete
- paradigms: Continuation-passing, Object-oriented, Dependency injection
- reference-distribution: Unlikely distribution
- entry @ esolangs.org
Sample program:
class Count(Count,Chain,Print,Add) extends Continuation
class CountForever(Count,Chain,Print,Add) extends Program {
Count c;
method continue(Passive accumulator) {
c = new Count(Passive,Count,Chain,Print,Add);
goto c.continue(new 1(Passive));
}
}
class Count() extends Continuation {
Count c;
Print p;
Add a;
method continue(Passive accumulator) {
c = new Count(Passive,Count,Chain,Print,Add);
a = new Add(Passive,Chain);
a.value = new 1(Passive);
a.next = c;
p = new Print(Passive,Chain);
p.next = a;
goto p.continue(accumulator);
}
}
Unlikely is a programming language that conflates objects with continuations, and methods with labels. It exposes program structures as objects with commensurate inheritance relationships. It also takes dependency injection to the logical extreme: if some class is used by an object, that class must be specified when the object is instantiated.
Reference Implementation: Coldwater
- license: BSD license
- implementation-type: static analyzer
- host-language: Python
Pixley
- type: Programming Language
- inception-date: May 2009
- genre: Esolang
- development-stage: mature
- computational-class: believed Turing-complete
- paradigms: Functional
- reference-distribution: Pixley distribution
- online @ catseye.tc
Sample program:
(let* ((a (lambda (x y) (cons x y)))) (a (quote foo) (quote ())))
Pixley is a very small subset of R5RS Scheme (or, if you prefer, R4RS Scheme), supporting only four datatypes (boolean, cons cell, function, and symbol) and only a dozen built-in symbols. The reference implementation of Pixley is written in 124 lines of Pixley (or, if you prefer, 124 lines of Scheme; and if you prefer more Scheme-ly metrics, it consists of 413 instances of 54 unique symbols in 684 cons cells.)
Reference Implementation: pixley.pix
- license: BSD license
- implementation-type: interpreter
- host-language: Pixley
Implementation: mignon
- license: BSD license
- implementation-type: interpreter
- host-language: ANSI C
Reference Implementation: haney
- license: BSD license
- implementation-type: interpreter
- host-language: Haskell
Reference Implementation: pixley.js
- license: BSD license
- implementation-type: interpreter
- host-language: JavaScript
- host-platform: HTML5
Implementation: pixley.pifx
- license: BSD license
- implementation-type: interpreter
- host-language: Pifxley
Reference Implementation: p-normal.pix
- license: BSD license
- implementation-type: compiler
- host-language: Pixley
- target-language: P-Normal Pixley
Crabwell
- type: Programming Language
- genre: Esolang
Crabwell is a dialect of Pixley which allows values to be bound to, not just symbols, but arbitrary S-expressions.
P-Normal Pixley
- type: Programming Language
- genre: Esolang
P-Normal Pixley is a simplified version of Pixley where let* can only bind one identifer
to one value and cond can only make one test, like Scheme's if.
Pifxley
- type: Programming Language
- genre: Esolang
Pifxley is a dialect of Pixley which supports an if construct instead of cond.
Dieter
- type: Programming Language
- inception-date: ca Oct 3, 2009
- genre: Experimental language
- development-stage: not fully complete
- computational-class: believed Turing-complete
- paradigms: Object-oriented
- reference-distribution: Dieter distribution
Sample program:
module beefy
procedure beef_up(x: ♥t): beefy ♥t
begin
return (bestow beefy x)
end
end.
Dieter (as in the German masculine given name Dieter, not dieter as in "one who diets") is a little experimental programming language that conflates type qualifiers with modules to produce something reminiscent of object-orientation. It demonstrates another way of thinking about objects, or rather, classes: not so much as aggregates of data as associations of predicates.
Dieter was intended as a way to make Hungarian notation part of the type system, and thus automatically checkable. However, it also suggests possible ways of dealing with the problems of aliasing — that is, determining if two pointers cannot possibly point to the same data, for safety and optimization considerations.
Reference Implementation: dieter.py
- license: BSD license
- implementation-type: typechecker
- host-language: Python
Etcha
- type: Programming Language
- inception-date: Oct 4, 2009
- genre: Esolang
- development-stage: mature
- computational-class: believed Turing-complete
- influences: BitChanger
- paradigms: Imperative
- reference-distribution: Etcha distribution
- entry @ esolangs.org
- online @ catseye.tc
- jnlp @ archive.org
Sample program:
>+++>+++>+++>+++>[+]>>>>+
Etcha is a two-dimensional descendant of Jeffry Johnston's BitChanger. Like BitChanger, it has four instructions; unlike BitChanger, its storage model is based on turtle graphics, which permits it to be immediately used for an alternative purpose: graphical composition. Unlike the turtle in LOGO however, the turtle in Etcha is an integral part of the computation, playing a role similar to the tape head of a Turing machine.
Reference Implementation: tc.catseye.etcha
- license: Public Domain
- implementation-type: interpreter
- host-language: Java
Implementation: tc.catseye.yoob.etcha
Implementation: etcha.js
- license: Public Domain
- implementation-type: interpreter
- host-language: JavaScript
- host-platform: HTML5
Implementation: etcha.lua
- license: Public Domain
- implementation-type: interpreter
- host-language: Lua
ZOWIE
- type: Programming Language
- inception-date: Dec 29, 2009
- genre: Esolang
- development-stage: mature
- computational-class: Turing-complete
- influences: BitChanger, SMITH
- paradigms: Imperative, Memory-mapped
- reference-distribution: ZOWIE distribution
- entry @ esolangs.org
- online @ catseye.tc
Sample program:
MOV R10, 90
MOV R1, R1
MOV R0, R10
MOV R8, R10
MOV R5, 1
MOV R10, R8
MOV R8, R10
MOV R5, 64
MOV R3, R8
ZOWIE is a machine-like language in which all operations including
structured control flow are memory-mapped. Control flow is structured in
the sense of structured programming — the programmer never deals with
gotos, or offsets or labels of any kind. Instead, the program writes to
a memory location to mark the beginning or end of a loop or conditional.
Reference Implementation: zowie.py
- license: Public Domain
- implementation-type: interpreter
- host-language: Python
Whothm
- type: Drawing Language
- inception-date: Jun 28, 2010
- genre: Esolang
- development-stage: mature
- computational-class: known not Turing-complete
- paradigms: Imperative
- reference-distribution: Whothm distribution
- online @ catseye.tc
- jnlp @ archive.org
Sample program:
r := (0, 0, 1, 2);
s := (0, 0, 1, 2);
XOR := TF/FT;
begin
r.x += r.w;
r.x += -1;
r.w += 1;
r.h += 1;
draw r, XOR;
s.x += s.w;
s.x += -1;
s.w += 1;
s.h += 2;
draw s, XOR;
end
Whothm is a simple language for describing infinite two-colour bitmapped drawings.
Reference Implementation: JWhothm
- license: BSD license
- implementation-type: interpreter
- host-language: Java
Implementation: whothm.lua
- license: BSD license
- implementation-type: interpreter
- host-language: Lua
Eightebed
- type: Programming Language
- inception-date: ca Sep 1, 2010
- genre: Esolang
- development-stage: mature
- computational-class: believed Turing-complete
- paradigms: Imperative
- reference-distribution: Eightebed distribution
- entry @ esolangs.org
Sample program:
type node struct {
int value;
ptr to node next;
};
var ptr to node jim;
var ptr to node george;
{
jim = malloc node;
if valid jim {
[@jim].value = (1 + 4);
george = jim;
}
if valid george {
print [@george].value;
}
free george;
free jim;
}
Eightebed is a small language with explicit malloc and free.
Through a modicum of static analysis
and runtime support, Eightebed is "safe": it is not possible to dereference a dangling
pointer or otherwise incorrectly-populated memory.
Eightebed was designed as a counter-example to Gregor Richards' claim that such
a language would either need a garbage collector, or not actually implement free.
Eightebed has a real free and has no garbage collector.
The name "Eightebed" came from a typo by Alise for the word "enlightened".
Reference Implementation: 8ebed2c.py
Oozlybub and Murphy
- type: Programming Language
- inception-date: Dec 2010
- genre: Esolang
- development-stage: not fully complete
- computational-class: ???
- paradigms: Imperative
- reference-distribution: Specs on Spec distribution
- entry @ esolangs.org
Sample program:
VARIABLES ARE p /p*/, p /q*/.
dynast(3) <->
(. do (. if? not? exists/dynast 5 ,then
create/countably/many/dynasts #myself#, 5 .) .) ,then
(. for each prime /p*|p/ below #myself#+2 do
for each prime /q*|q/ below /p*|pp/+1 do
if? not? exists/dynast /p*|p|p/+/q*|q|q/ ,then
copy/dynast #myself#, /p*|ppp/, /q*|qqq/ .)
The name of this language is Oozlybub and Murphy. Despite appearances, this name refers to a single language. The majority of the language is named Oozlybub. The fact that the language is not entirely named Oozlybub is named Murphy. Deal with it. For the sake of providing an "olde tyme esoterickal de-sign", the language combines several unusual features, including multiple interleaved parse streams, infinitely long variable names, gratuitously strong typing, and only-conjectural Turing completeness.
Gemooy
- type: Programming Language
- inception-date: Dec 2, 2010
- genre: Esolang
- development-stage: mature
- computational-class: Turing-complete
- influences: 2-ill, Etcha
- paradigms: Imperative
- reference-distribution: Gemooy distribution
- entry @ esolangs.org
- online @ catseye.tc
- jnlp @ archive.org
Sample program:
%### # ### # # ### # ### # # ### # ###@
@ @# @
@ @ @
@@
@ @
$ @# # @
# @
#
@ @
@
@
#
#
@
@ @
@# @
@ @
@
@ @#@
Gemooy is a 2-dimensional esolang with 3 instructions (5 initial symbols) which combines features from 2-ill and Etcha, and adds self-modification. It came about when the author noticed the tape-related semantics of 2-ill were essentially the same as those of BitChanger.
Reference Implementation: gemooy.js
- license: Public Domain
- implementation-type: interpreter
- host-language: JavaScript
- host-platform: HTML5
Implementation: gemooy.lua
- license: Public Domain
- implementation-type: interpreter
- host-language: Lua
Implementation: tc.catseye.yoob.gemooy
Nhohnhehr
- type: Programming Language
- inception-date: Dec 8, 2010
- genre: Esolang
- development-stage: mature
- computational-class: can simulate some push-down automata
- paradigms: 2-dimensional
- reference-distribution: Nhohnhehr distribution
- entry @ esolangs.org
Sample program:
+------+
| /}|
|&#/$?@|
| / \&|
| |
| { |
|\\ |
+------+
Nhohnhehr is a remotely fungeoid language which explores the design space between having a fixed playfield versus an expandable one. When the instruction pointer reaches the edge of the playfield (the "room"), whether it wraps around or creates a new room and adjoins it to that edge, depends on the current edge mode of the program. New copies of rooms may be rotated before being adjoined to existing rooms, but rooms are otherwise immutable.
Reference Implementation: nhohnhehr.py
- license: Public Domain
- implementation-type: interpreter
- host-language: Python
Kelxquoia
- type: Programming Language
- inception-date: Dec 23, 2010
- genre: Esolang
- development-stage: not fully complete
- computational-class: believed Turing-complete
- paradigms: 2-dimensional, Grid-rewriting, Self-modifying
- reference-distribution: Kelxquoia distribution
Sample program:
>+-0 0*+-1*/+-?*-R*- *+-?*-R*-?*/v
RRRRRRRRRRRRRRRRRRRR RRRRRRRRRRRRR
$>+-0 0*+-1*/+-?*-R*- *+-?*-R*-?*/v
' ' ' ' ' '
' ' '
^ /*?-*P-*?-+*?-*P-* -+ <
P PPPPPPPPPPPPPPPPPP PP P
^ /*?-*P-*?-+*?-*P-* -+ <
00 00 00 00
Kelxquoia is another remotely fungeoid language, this one self-modifying — in fact, self-destroying. As instructions are executed, they are erased. In order to execute indefinitely, new instructions of some sort must be created. Luckily the language provides as its main data-manipulation facility, grid-rewriting, which can be used to restore instructions that were previously erased after execution.
Wunnel
- type: Programming Language
- inception-date: Feb 13, 2011
- genre: Esolang
- development-stage: mature
- computational-class: believed Turing-complete
- influences: 1L, reMorse
- paradigms: Turning tarpit
- reference-distribution: Wunnel distribution
- entry @ esolangs.org
- online @ catseye.tc
- jnlp @ archive.org
Sample program:
o ooo o
o
o
o
o o
o o
o o
o o
o
o o o
o o
o
o o
o o
o o o
o o
o
o oooooooo o
o
o
o
o oooo o
Wunnel is a two-dimensional language which draws from the 1L family of languages and incorporates features from reMorse. The name is both a play on the pronunciation of "1L", and a recursive portmanteau of the words Wunnel and tunnel which is used to describe the long sequences of identical instructions (often nops) used in Wunnel programs to sync up remote parts of the program.
Reference Implementation: tc.catseye.yoob.wunnel
Implementation: wunnel.js
- license: Public Domain
- implementation-type: interpreter
- host-language: JavaScript
- host-platform: HTML5
Implementation: wunnel.lua
- license: Public Domain
- implementation-type: interpreter
- host-language: Lua
Pail
- type: Programming Language
- inception-date: May 25, 2011
- genre: Esolang
- development-stage: mature
- computational-class: believed Turing-complete
- influences: Pixley
- paradigms: Functional
- reference-distribution: Pail distribution
- entry @ esolangs.org
- online @ catseye.tc
Sample program:
**[*let [
[cadrg *[#fst ##*[#snd #g]]]
**[*let [
[g [x [y z]]]
***cadrg
]]
]]
Pail is a programming language based on pairs; just as Lisp stands for LISt Processing, Pail stands for PAIr Language. Its original working title was "Bizaaro[sic]-Pixley", as it attempts to resemble Pixley while turning several concepts on their heads: use pairs instead of lists, quote by default instead of eval by default, and allow not just values but also names of bindings to be expressed.
"Pail is an acceptable Bizaaro[sic]-Pixley" is a reference to an article called "Ruby is an acceptable Lisp".
Reference Implementation: Pail.lhs
- license: BSD license
- implementation-type: interpreter
- host-language: Haskell (Literate Haskell)
Xoomonk
- type: Programming Language
- inception-date: Aug 7, 2011
- genre: Esolang
- development-stage: mature
- computational-class: believed Turing-complete
- paradigms: Imperative, Lazy
- reference-distribution: Xoomonk distribution
- entry @ esolangs.org
Sample program:
l := $loop*
counter := 5
l.do := {
y := x
print ^.counter
o := $sub*
o.x := ^.counter
o.y := 1
^.counter := o.result
continue := o.result
}
Xoomonk is a programming language in which malingering updatable stores are first-class objects. Malingering updatable stores unify several language constructs, including procedure activations, named parameters, and object-like data structures.
The Xoomonk project was also an experiment in test-driven language design. The specification is largely composed of a number of example programs in the format of Falderal tests, which were written while the language was being designed. These were used to compare the reference implementation, while it was being developed, against the spec.
Reference Implementation: xoomonk.py
- license: BSD license
- implementation-type: interpreter
- host-language: Python
Flobnar
- type: Programming Language
- inception-date: Oct 28, 2011
- genre: Esolang
- development-stage: not fully complete
- computational-class: believed Turing-complete
- influences: Befunge-93
- paradigms: Functional, 2-dimensional
- reference-distribution: Flobnar distribution
- entry @ esolangs.org
- online @ catseye.tc
Sample program:
> v
^\ <
:v v \<@
-< : 6
1 : > *
-| <
11
One day in September of 2011 — though I'm not sure precisely which one — marked Befunge-93's 18th birthday. That means that Befunge is now old enough to drink in its native land of Canada. To celebrate this, I thought I'd get Befunge-93 drunk to see what would happen. What happened was Flobnar, an esolang which is in many respects a functional dual of Befunge-93; most of the symbols have analogous meanings, but execution proceeds in a much more dataflow-like fashion.
Reference Implementation: Flobnar.hs
- license: BSD license
- implementation-type: interpreter
- host-language: Haskell
Madison
- type: Proof Language
- inception-date: Dec 2, 2011
- genre: DSL
- development-stage: unfinished
- computational-class: believed Turing-complete
- paradigms: Proof checking, Term-rewriting
- reference-distribution: Specs on Spec distribution
Sample program:
type tree is
tree(leaf) -> true
tree(branch(X,Y)) -> and(tree(X),tree(Y))
in let
reflect(leaf) -> leaf
reflect(branch(A,B)) -> branch(reflect(B),reflect(A))
in theorem
forall X where tree(X)
reflect(reflect(X)) ~> X
proof
case X = leaf
reflect(reflect(leaf))
-> reflect(leaf) [by reflect.1]
-> leaf [by reflect.1]
case X = branch(S, T)
reflect(reflect(branch(S, T)))
-> reflect(branch(reflect(T),reflect(S))) [by reflect.2]
-> branch(reflect(reflect(S)),reflect(reflect(T))) [by reflect.2]
-> branch(S,reflect(reflect(T))) [by IH]
-> branch(S,T) [by IH]
qed
Madison was an experiment in designing a language in which one can state proofs of properties of term-rewriting systems. Classical methods of automated reasoning, such as resolution, are not used; indeed, term-rewriting itself is used to check the proofs. Both direct proof and proof by induction are supported. Induction in a proof must be across a structure which has a well-founded inductive definition. Such structures can be thought of as types, although this is largely nominal; the traditional typelessness of term-rewiting systems is largely retained.
This design never got to the point where I thought I could implement it, but influenced Maxixe.
Robin
- type: Programming Language
- inception-date: 2011
- genre: Production language
- development-stage: unfinished
- paradigms: Functional
- reference-distribution: Robin distribution
- online @ catseye.tc
Sample program:
(require multiply)
(define fact (fun (self n)
(multiply n
(if (gt? n 1)
(self self (subtract n 1))
1))))
(display (fact fact 5))
Robin is a functional programming language with eager evaluation, latent typing, and a homoiconic syntax (see Scheme), based on a radically simple core semantics (see Pixley) in which both functions and macros are defined in terms of a more basic abstraction, the fexpr.
Expressions in Robin are referentially transparent; programs interact with the outside world through an event-oriented framework.
Robin was originally a design for a Pixley-based operating system (or something similar to an operating system) which was heavily resource-oriented; almost everything, including every concurrent process, was a virtual device which must be acquired from a central resource arbiter. This arbiter could satisfy the constraints specified when requesting a device any way it saw fit; so the operating environment potentially had a lot of influence over exactly what any given program does.
Not a lot of that idea remains, but it did influence the fact that Robin should be a purely functional language which nevertheless interacts with the rest of the world through some kind of framework. After much consideration, the framework arrived at is very similar to that used in The Elm Architecture.
Reference Implementation: Language.Robin
- license: BSD license
- implementation-type: interpreter
- host-language: Haskell
Troupe
- type: Programming Language
- inception-date: Jun 25, 2012
- genre: Esolang
- development-stage: not fully complete
- computational-class: believed Turing-complete
- paradigms: Imperative, State machine
- reference-distribution: Troupe distribution
Troupe is an esolang based on hedgehogs, faery rings, and hills. It maps fairly neatly to the definition of a Turing machine, so it is almost certainly Turing-complete.
Velo
- type: Programming Language
- inception-date: Jul 2012
- genre: Esolang
- development-stage: not fully complete
- computational-class: believed Turing-complete
- influences: Ruby
- paradigms: Object-oriented
- reference-distribution: Velo distribution
- online @ catseye.tc
Sample program:
yes = {IO.print {Yes}}
no = {IO.print {No}}
if ({X}.equals {Y}), yes, no
Velo is a vaguely Ruby-inspired "scripting" language which unifies
strings with code blocks, and scripts with object classes. Curly braces
delimit string literals, and there is no difference between a string literal
and a block of code given to, say, an if statement. Any given script is
an object, which inherits from the root object in delegation-OO style.
Reference Implementation: velo.rb
- license: BSD license
- implementation-type: interpreter
- host-language: Ruby
Implementation: velo.lua
- license: BSD license
- implementation-type: interpreter
- host-language: Lua
Exanoke
- type: Programming Language
- inception-date: ca Jul 2012
- genre: Experimental language
- development-stage: mature
- computational-class: Primitive recursive
- paradigms: Functional
- reference-distribution: Exanoke distribution
- entry @ esolangs.org
Sample program:
def inc(#)
cons(:one, #)
def add(#, other)
if eq?(#, :nil) then other else self(<tail #, inc(other))
def mul(#, other)
if eq?(#, :nil) then :nil else
add(other, self(<tail #, other))
def fact(#)
if eq?(#, :nil) then cons(:one, :nil) else
mul(#, self(<tail #))
def four(#)
cons(:one, cons(:one, cons(:one, cons(:one, #))))
fact(four(:nil))
Exanoke is a functional language which is syntactically restricted to expressing the primitive recursive functions.
Reference Implementation: exanoke.py
- license: BSD license
- implementation-type: interpreter
- host-language: Python
Cfluviurrh
- type: Programming Language
- inception-date: Aug 26, 2012
- genre: Esolang
- development-stage: mature
- computational-class: believed Turing-complete
- paradigms: Imperative
- reference-distribution: Cfluviurrh distribution
- entry @ esolangs.org
- online @ archive.org
Sample program:
(print ASCII table while experiencing a bewildering array of emotions)
a=8
a*=8
b=a
b+=a
b-=2
:X
a+=1
a>
z@=X
z?a<b
Cfluviurrh is, as far as I am aware, the first programming language designed for writing programs that can feel. Cfluviurrh defines a mechanism by which a program can be instructed to experience particular emotions.
You might, thus, on first blush, consider Cfluviurrh to be unimplementable, as modern-day computers are not capable of experiencing emotions (you guess.) However, this is demonstrably untrue. The reference interpreter demonstrates it.
Reference Implementation: cfluviurrh
- license: BSD license
- implementation-type: interpreter
- host-language: ANSI C
Jolverine
- type: Programming Language
- inception-date: Sep 10, 2012
- genre: Esolang
- development-stage: mature
- computational-class: Turing-complete
- influences: Wunnel, Half-Broken Car in Heavy Traffic
- paradigms: Turning tarpit, 2-dimensional
- reference-distribution: Jolverine distribution
- entry @ esolangs.org
Sample program:
--*-*
\
\
\ *
\ /
\ /
\ /
* /
\ /
*-*---*
The Jolverine language was devised as a conscious attempt to expand the genre of turning tarpit by adding the feature of modifying the instruction wheel during execution.
The name is a portmanteau of "jolly wolverine" (where "jolly" is a euphemism for "drunk",) which is an attempt to capture, in a noun phrase, the language's vicious, erratic nature.
Reference Implementation: jolverine.py
- license: Public Domain
- implementation-type: interpreter
- host-language: Python
SICKBAY
- type: Programming Language
- inception-date: Sep 22, 2012
- genre: Esolang
- development-stage: mature
- computational-class: Turing-complete
- paradigms: Imperative
- reference-distribution: SICKBAY distribution
- entry @ esolangs.org
Sample program:
10 LET B% = 99
(100+B%) END
100 GOTO 200:REM BEGIN LOOP
200 PRINT B%;:PRINT " BOTTLES OF BEER ON THE WALL,"
205 PRINT B%;:PRINT " BOTTLES OF BEER,"
210 PRINT "TAKE ONE DOWN, PASS IT AROUND,"
215 LET B% = (B% - 1)
220 PRINT B%;:PRINT " BOTTLES OF BEER ON THE WALL.":PRINT ""
230 GOTO 100
SICKBAY is an esoteric dialect of BASIC with a call ring buffer instead of
a call stack, and computed line number definitions (and no IF because
of that.)
Reference Implementation: SAWBONES
- license: Public Domain
- implementation-type: interpreter
- host-language: Python
Carriage
- type: Programming Language
- inception-date: Nov 2012
- genre: Esolang
- development-stage: not fully complete
- computational-class: unknown computational class
- paradigms: Concatenative
- reference-distribution: Carriage distribution
- entry @ esolangs.org
- online @ catseye.tc
Sample program:
111-@11-~!$11111++++11-~@11-~!
Carriage is the result of various, not-entirely-successful attempts to design a "pure" concatenative language — one in which the program texts are monoids and nothing but monoids (no quoting operators or the like.) The result was midly unusual — subroutines are specified by indices into an area of the stack which contains program symbols, thus may overlap — and was released as an esolang.
Reference Implementation: Carriage.hs
- license: Public Domain
- implementation-type: interpreter
- host-language: Haskell
Castile
- type: Programming Language
- inception-date: Nov 21, 2012
- genre: Experimental language
- development-stage: not fully complete
- computational-class: believed Turing-complete
- influences: ANSI C, Eightebed, Rust
- paradigms: Imperative, Functional
- etymology: soap
- reference-distribution: Castile distribution
Sample program:
fun foo(a, b: integer|string) {
r = a;
typecase b is integer {
r = r + b;
};
typecase b is string {
r = r + len(b);
};
r
}
main = fun() {
a = foo(a, 333 as integer|string);
a = foo(a, "hiya" as integer|string);
a /* should output 337 */
}
Castile is a simple imperative language with union types. It exists mainly
because an interpreter-plus-compiler for it was written. It is
a bit like ANSI C except with proper union types (and no typecasts.) Null
pointer dereferencing is thus prevented because "null" is a separate type in
the union that must be selected explicitly with a typecase form. Local
variables are mutable, but arguments and globals aren't. The compiler
supports several backends, including ANSI C, JavaScript, and Ruby.
Reference Implementation: castile (Python)
- license: BSD license
- implementation-type: interpreter-plus-compiler
- host-language: Python
- target-languages: ANSI C, JavaScript, Ruby, stackmac
SixtyPical
- type: Programming Language
- inception-date: Mar 31, 2014
- genre: Machine language
- paradigms: Imperative
- etymology: portmanteau
- reference-distribution: SixtyPical distribution
Sample program:
byte table screen @ 1024
routine main
trashes a, x, z, n, screen
{
ld x, 0
ld a, 83 // 83 = screen code for heart
repeat {
st a, screen + x
inc x
} until z
}
SixtyPical is a very low-level programming language, similar to 6502 assembly, which defines a set of static analyses via type-checking and abstract interpretation (liveness analysis of variables, i.e. memory locations.)
Reference Implementation: sixtypical (Python)
- license: BSD license
- host-language: Python
- implementation-type: compiler
- target-language: 6502 machine code
Implementation: sixtypical (Haskell)
- license: BSD license
- host-language: Haskell
- implementation-type: compiler
- target-language: Ophis Assembler
Tamsin
- type: Programming Language
- inception-date: Apr 27, 2014
- genre: Experimental language
- development-stage: unfinished
- paradigms: Functional, Logic programming, Metalanguage
- etymology: feminine given name
- reference-distribution: Tamsin distribution
Sample program:
main = expr0 → E & walk(E).
expr0 = expr1 → E1 & {"+" & expr1 → E2 & E1 ← add(E1,E2)} & E1.
expr1 = term → E1 & {"*" & term → E2 & E1 ← mul(E1,E2)} & E1.
term = "x" | "y" | "z" | "(" & expr0 → E & ")" & E.
walk(add(L,R)) = walk(L) → LS & walk(R) → RS & return LS+RS+' +'.
walk(mul(L,R)) = walk(L) → LS & walk(R) → RS & return LS+RS+' *'.
walk(X) = return ' '+X.
Tamsin is an oddball little language that can't decide if it's a meta-language, a programming language, or a rubbish lister. Its primary goal is to allow the rapid development of parsers, static analyzers, interpreters, and compilers, and to allow them to be expressed compactly.
Reference Implementation: tamsin.py
- license: BSD license
- host-language: Python
- implementation-type: interpreter
Kind of compiles, too.
Implementation: tamsin.tamsin
- license: BSD license
- host-language: Tamsin
- implementation-type: compiler
- target-language: C99
Yolk
- type: Programming Language
- inception-date: Aug 24, 2014
- genre: Esolang
- development-stage: mature
- computational-class: believed Turing-complete
- paradigms: Functional, Meta-circular
- reference-distribution: Yolk distribution
- entry @ esolangs.org
Sample program:
(ifeq (head arg) (quote arg)
(head (tail (tail arg)))
(ifeq (head (head arg)) (quote head)
(head (self (cons (head (tail (head arg))) (tail arg))))
(ifeq (head (head arg)) (quote tail)
(tail (self (cons (head (tail (head arg))) (tail arg))))
(ifeq (head (head arg)) (quote cons)
(cons (self (cons (head (tail (head arg))) (tail arg))) (self (cons (head (tail (tail (head arg)))) (tail arg))))
(ifeq (head (head arg)) (quote quote)
(head (tail (head arg)))
(ifeq (head (head arg)) (quote ifeq)
(ifeq (self (cons (head (tail (head arg))) (tail arg)))
(self (cons (head (tail (tail (head arg)))) (tail arg)))
(self (cons (head (tail (tail (tail (head arg))))) (tail arg)))
(self (cons (head (tail (tail (tail (tail (head arg)))))) (tail arg))))
(ifeq (head (head arg)) (quote self)
(self (cons (head (tail arg))
(cons (head (tail arg))
(cons (self (cons (head (tail (head arg))) (tail arg))) (tail (quote (tail)))))))
(ifeq))))))))
Yolk is a tiny S-expression-based programming language (or computational calculus) with a tiny meta-circular interpreter.
Reference Implementation: yolk.py
- license: BSD license
- implementation-type: interpreter
- host-language: Python
Reference Implementation: yolk.yolk
- license: BSD license
- implementation-type: interpreter
- host-language: Yolk
Matchbox
- type: Programming Language
- inception-date: Feb 2015
- genre: Pedagogical language
- development-stage: mature
- computational-class: ???
- paradigms: Imperative
- reference-distribution: Matchbox distribution
- online @ catseye.tc
Sample program:
MOV 1, M0
MOV 1, M2
WAIT M1, 0
WAIT M2, 0
; begin c.s.
MOV M3, R0
INC R0
MOV R0, M3
; end c.s.
MOV 0, M0
A toy language for a toy race-condition finder.
I wrote this because I feel race conditions are an underappreciated problem in software development. In programming education, they're often not given the attention they deserve, given that they are a real problem that comes up once you get into any kind of concurrent programming — and one that can very difficult to pinpoint, much less fix.
The general "someone else's problem"-ness surrounding race conditions seems to have fostered two misconceptions in particular that I wanted to highlight.
Even though Matchbox is an assembly-like language, race conditions are not restricted to machine language. Nearly every high-level programmer works with either filesystems or databases, and those are both basically gigantic tracts of shared memory. Race conditions are just waiting to happen, if you're not careful.
And there is sometimes the impression that the only way to protect oneself against race conditions is if the system provides an atomic-test-and-set-like operation. If such an operation is avaiable, you should probably use it, but it's not the only way. There are several different programming methods for guaranteeing mutually exclusive access to a resource, even when such operations are not available. These were developed before such operations were widely available in hardware, and although they are largely of historical interest, they also posess a certain conceptual beauty. One such method is Peterson's Algorithm, which Matchbox can run and show correct.
Implementation: matchbox.js
- license: Public Domain
- implementation-type: static analyzer
- host-language: JavaScript
- host-platform: HTML5
SITU-SOL
- type: Programming Language
- inception-date: Jul 2015
- genre: Esolang
- development-stage: not fully complete
- computational-class: Turing-complete
- paradigms: Imperative, Stack-based
- reference-distribution: SITU-SOL distribution
- online @ archive.org
SITU-SOL is a vaguely Forth-like language which was designed and implemented (by hand!) during RetroChallenge 2015/07, and entered into an emulated Commodore 64 using SITU-MON.
Reference Implementation: SITU-SOL (Commodore 64)
- license: Unknown license
- implementation-type: compiler
- host-language: 6502 machine code
- target-language: 6502 machine code
Samovar
- type: Programming Language
- inception-date: 2016
- genre: DSL
- development-stage: basically complete
- computational-class: unknown computational class
- influences: Madison
- paradigms: Probabilistic, Logic programming, State machine
- reference-distribution: Samovar distribution
Sample program:
rules
[actor(α),item(β),¬holding(α,β)] α picks up the β. [holding(α,β)]
[actor(α),item(β),holding(α,β)] α puts down the β. [¬holding(α,β)]
end
situations
[actor(Ignatz),item(brick)]
end
Samovar is a DSL for world-modeling using propositions rather than explicit objects. It could be thought of as an "assertion-retraction engine", which itself could be thought of as a very stilted style of Prolog programming plus some syntactic sugar.
Reference Implementation: samovar (Python)
- license: Public Domain
- implementation-type: interpreter
- host-language: Python
Maxixe
- type: Proof Language
- inception-date: 2016
- genre: Experimental language
- development-stage: basically complete
- computational-class: believed Turing-complete
- influences: Madison
- paradigms: Proof checking, Natural deduction
- reference-distribution: Maxixe distribution
Sample program:
given
Modus_Ponens = impl(P, Q) ; P |- Q
Simplification = and(P, Q) |- Q
Commutativity_of_Conjunction = and(P, Q) |- and(Q, P)
Premise = |- and(p, impl(p, q))
show
q
proof
Step_1 = and(p, impl(p, q)) by Premise
Step_2 = and(impl(p, q), p) by Commutativity_of_Conjunction with Step_1
Step_3 = impl(p, q) by Simplification with Step_1
Step_4 = p by Simplification with Step_2
Step_5 = q by Modus_Ponens with Step_3, Step_4
qed
Maxixe is a simple, generalized proof-checking language. Given a proof written out fully and explicitly (including all rules of inference), a computer can check if it is valid or not. Since Maxixe has no built-in rules of inference, it is in this manner not restricted to using a particular kind of logic — it ought to be possible to implement propositional logic, predicate logic, equational logic in it (and fragments and combinations thereof).
Reference Implementation: maxixe (Python)
- license: Public Domain
- implementation-type: interpreter
- host-language: Python
Equipage
- type: Programming Language
- inception-date: May 14, 2018
- genre: Esolang
- development-stage: mature
- computational-class: believed Turing-complete
- influences: Carriage
- paradigms: Functional, Concatenative
- reference-distribution: Equipage distribution
- entry @ esolangs.org
- online @ catseye.tc
Sample program:
1~%1-1-1-~;
.!.!.!.!.!.!.!.!.!.!
$11-1-~;
.!.!.!.!.!.!.!
1$
.!
11+11-11+1
.!.!.!.!.!.!.!.!.!
!
11-1-~;
.!.!.!.!.!.!
!
Equipage is a "pure" concatenative programming language — program texts are monoids and nothing but monoids (no quoting operators or the like.) It is the language that Carriage might've been, if I had not been so concerned about quoting at the time.
Reference Implementation: Equipage.hs
- license: Public Domain
- implementation-type: interpreter
- host-language: Haskell
Implementation: equipage.py
- license: Public Domain
- implementation-type: interpreter
- host-language: Python
Wanda
- type: Programming Language
- inception-date: Feb 27, 2019
- genre: Esolang
- development-stage: mature
- computational-class: believed Turing-complete
- paradigms: Concatenative (nominally), String-rewriting
- reference-distribution: Wanda distribution
- entry @ esolangs.org
- online @ catseye.tc
Sample program:
$
: 0 $ fact -> $ 1 ;
: $ fact -> $ dup 1 - fact * ;
5 fact
Wanda is a Forth-like, "concatenative" programming language that's arguably not concatenative at all, nor even "stack-based", because it's based on a string-rewriting semantics.
Reference Implementation: wanda.lua
- license: Public Domain
- implementation-type: interpreter
- host-language: Lua
Wagon
- type: Programming Language
- inception-date: Aug 13, 2019
- genre: Esolang
- development-stage: mature
- computational-class: Turing-complete
- paradigms: Functional, Concatenative
- reference-distribution: Wagon distribution
- entry @ esolangs.org
- online @ catseye.tc
Sample program:
p@ I I I SII SII
Wagon is a purely concatentive (in the sense of Equipage) language which is "second-order concatenative": instead of functions which take states to states, the symbols of the language represent functions which take functions from states to states, to functions that take states to states.
The hope in designing it was that the second-order status would allow control structures to be embedded in the program. It does allow this, but it does not allow arbitrary control structures. Nevertheless, it has been shown to be Turing-complete, as arbitrary Tag systems can be compiled to Wagon.
Reference Implementation: Language.Wagon
- license: BSD license
- implementation-type: interpreter
- host-language: Haskell
Oxcart
- type: Programming Language
- inception-date: Oct 28, 2019
- genre: Esolang
- development-stage: mature
- computational-class: believed Turing-complete
- paradigms: Functional, Concatenative, Continuation-passing
- reference-distribution: Oxcart distribution
- entry @ esolangs.org
- online @ catseye.tc
Sample program:
<0^^^^^^^^^^>S:<:v:)%
Oxcart is another purely concatenative (in the sense of Equipage) language; but this time it's a continuation-passing concatenative language. Instead of functions which take states to states, the symbols of the language represent functions which are written in continuation-passing style (CPS), i.e. they take two arguments: a state and a continuation. A special form of function composition is used to compose two such functions, and it has an identity and forms a monoid like conventional function composition.
Reference Implementation: Language.Oxcart
- license: BSD license
- implementation-type: interpreter
- host-language: Haskell
Tandem
- type: Programming Language
- inception-date: June 2020
- genre: Esolang
- development-stage: mature
- computational-class: Turing-complete
- paradigms: String-rewriting
- reference-distribution: Tandem distribution
- entry @ esolangs.org
- online @ catseye.tc
Sample program:
{B:I,O}
Q → 0 &
O → N &
(
Q0 → 1 & Ic… → … |
Q1 → 2 & Ia… → … |
Q1 → 2 & Io… → … |
Q2 → 3 & It → & O… → Y
)*
Tandem is an experimental rewriting language where the rewrite rules form a Kleene algebra. The object being rewritten by a Tandem program is a collection of labelled stacks — a finite mapping from strings to strings. The strings are always rewritten at the left edge, so they are effectively stacks.
Writing finite automata, push-down automata, Turing machines, and other automata is quite natural in Tandem,
because transition rules such as "In state 4, if the next character in the input is g, consume it and
push $ onto the stack and go to state 9" translate quite straightforwardly to rewrite rules such as
Q4 → 9 & Ig… → … & K… → $…
Reference Implementation: Language.Tandem
- license: Public Domain
- implementation-type: interpreter
- host-language: Haskell
Lanthorn
- type: Programming Language
- inception-date: Feb 2021
- genre: Esolang
- development-stage: mature
- computational-class: believed Turing-complete
- paradigms: Functional
- reference-distribution: Lanthorn distribution
Sample program:
letrec
odd = fun(x) -> if eq(x, 0) then false else even(sub(x, 1))
even = fun(x) -> if eq(x, 0) then true else odd(sub(x, 1))
in
even(6)
Lanthorn is a purely functional toy programming language in which
letrec is mere syntactic sugar. In it is demonstrated a transformation
from letrec to let that is purely syntactic, and which turns the
sample program shown above, into this:
let
odd$0 = fun(x, odd$1, even$1) -> let
odd = fun(x$1) -> odd$1(x$1, odd$1, even$1)
even = fun(x$1) -> even$1(x$1, odd$1, even$1)
in
if eq(x, 0) then false else even(sub(x, 1))
even$0 = fun(x, odd$1, even$1) -> let
odd = fun(x$1) -> odd$1(x$1, odd$1, even$1)
even = fun(x$1) -> even$1(x$1, odd$1, even$1)
in
if eq(x, 0) then true else odd(sub(x, 1))
odd = fun(x) -> odd$0(x, odd$0, even$0)
even = fun(x) -> even$0(x, odd$0, even$0)
in
even(6)
Reference Implementation: Language.Lanthorn
- license: MIT license
- implementation-type: interpreter
- host-language: Haskell
Vinegar
- type: Programming Language
- inception-date: Nov 2021
- genre: Esolang
- development-stage: not fully complete
- computational-class: believed Turing-complete
- paradigms: Concatenative
- reference-distribution: Vinegar distribution
Sample program:
fact =& fac1 fac2;
fac1 =& dup int[0] gt!;
fac2 =| fac3 fac4;
fac3 =& dup int[1] eq!;
fac4 =& pop dup int[1] sub fact mul;
main =& int[5] fact;
Vinegar is a "semi-concatenative" language where every operation can fail.
"Semi-concatenative" is supposed to mean that there isn't just the usual
implicit "concatenate" program-composing operator, there's also a second
program-composing operator, "alternate" (notated explicitly by |).
This second operator is intended to gracefully handle the case where a program operation has failed -- which any of them can.
Although the second operator is notated explicitly, the language supports a syntax variation (shown above) where both operators can be used implicitly... as long as each definition is introduced appropriately.
Reference Implementation: vinegar (Python)
- license: BSD license
- implementation-type: interpreter
- host-language: Python
Eqthy
- type: Proof Language
- inception-date: ca Jun 2022
- genre: Minimal language
- development-stage: work in progress
- computational-class: believed Turing-complete
- paradigms: Proof checking, Equational logic
- reference-distribution: Eqthy distribution
Sample proof:
axiom (idright) mul(A, e) = A
axiom (idleft) mul(e, A) = A
axiom (assoc) mul(A, mul(B, C)) = mul(mul(A, B), C)
theorem (idcomm)
mul(A, e) = mul(e, A)
proof
A = A
mul(A, e) = A [by idright]
mul(A, e) = mul(e, A) [by idleft]
qed
Eqthy is a formalized language for proofs in equational logic. Its design attempts to reconcile simplicity of implementation on a machine with human usability.
On one hand, it is possible (and only somewhat tedious) for humans to read Eqthy proofs, and to write them by hand. On the other hand, a checker for Eqthy proofs has been written in Python, in about 550 lines of code; the core verifier module is less than 200 lines of code.
Reference Implementation: eqthy (Python)
- license: BSD license
- implementation-type: verifier
- host-language: Python
Fountain
- type: Meta-language
- inception-date: 2023
- genre: Experimental language
- development-stage: unfinished
- paradigms: Metalanguage
- reference-distribution: Fountain distribution
Sample program:
Goal<n> ::=
<. a = 0 .> { "a" <. a += 1 .> } <. a = n .>
<. b = 0 .> { "b" <. b += 1 .> } <. b = n .>
<. c = 0 .> { "c" <. c += 1 .> } <. c = n .>
;
Fountain is a grammar formalism capable of expressing context-sensitive languages (CSLs), and supporting both efficient parsing and efficient generation of strings in to those languages.
The example grammar above both parses and generates strings of
the classic CSL a^n b^n c^n. In both directions it
operates deterministically, and thus efficiently, guided by the
interspersed semantic constraints.
Reference Implementation: fountain
- license: BSD license
- host-language: Haskell
- implementation-type: parser, generator
Argyle
- type: Programming Language
- inception-date: Dec 2024
- genre: Experimental language
- development-stage: unfinished
- paradigms: Functional, Reflective
- reference-distribution: Argyle distribution
Sample program:
(let ((cons
(lambda (x y)
(subst (subst (stencil (x y) (x y)) "x" (abt x)) "y" (abt y))))
(car
(lambda (lst)
(destruct-abt lst
(lambda (name) (neg 1))
(lambda (val) (neg 2))
(lambda (param body) (neg 3))
(lambda (name expr body) (neg 4))
(lambda (fn arg) (eval fn))
(lambda (name arg) (neg 6)))))
(cdr
(lambda (lst)
(destruct-abt lst
(lambda (name) (neg 1))
(lambda (val) (neg 2))
(lambda (param body) (neg 3))
(lambda (name expr body) (neg 4))
(lambda (fn arg) (eval arg))
(lambda (name arg) (neg 6)))))
(lst (cons 1 (cons 2 (cons 3 0)))))
(car (cdr lst)))
Argyle is a Lisp-like programming language which is homoiconic at a higher level than Lisp: an Argyle program is represented as an Abstract Binding Tree (ABTs), and ABTs are first-class values. These ABTs are also hygienic in the sense that all defined ABT operations are (quite unlike Lisp's cons-lists) designed to preserve their name-binding structure throughout all operations on them.
Reference Implementation: argyle
- license: BSD license
- host-language: Haskell
- implementation-type: interpreter
UampirNexol
- type: Programming Language
- inception-date: Feb 2025
- genre: Machine language, Experimental language
- development-stage: unfinished
- influences: SixtyPical
- paradigms: Functional, Imperative
- reference-distribution: UampirNexol distribution
Sample program:
let
chrout = extern @0xffd2 : State[A/] -> State[/A]
in
LDA# 40 ; (call chrout) ;
LDA# 41 ; (call chrout) ;
LDA# 42 ; (call chrout)
UampirNexol is a language in which MOS 6502 machine language programs can be expressed as functions which map machine states to machine states. These functions are used as combinators which are composed in the manner of function-level programming. A complete program is also a function that maps machine states to machine states Once a complete program is constructed, real 6502 machine code can then be extracted from that function, and executed on a 6502-based computer.
UampirNexol is a proof-of-concept implementation of the Machine State Combinators concept, which is where the lines of research discussed in the Future directions for SixtyPical document ended up.
Reference Implementation: uampirnexol
- license: BSD license
- host-language: Haskell
- implementation-type: compiler
About these Languages
Most of these languages are programming languages, or at least "computer languages" of some kind, although some of them have not been implemented on a computer (or may even be unimplementable on a computer), and at least one of them is a conlang. Many of them are esolangs.
If it was implemented by Cat's Eye Technologies, but was designed by someone else, it won't be on this list, it'll be here instead: Language Implementations.
If it was implemented by Chris Pressey, but not under the auspices of Cat's Eye Technologies, it won't be on this list.
Some of these languages have interpreters that can run online, in your web browser. (Look for the Try it Online button). By selecting sample programs and watching them run, you can gain an appreciation of how the language works; by composing your own programs, you can gain an even better appreciation.
You may also be interested in reading about what it was like to design these or the ones that got away.